• 梯度不稳定

    • 在深度神经网络中，梯度是不稳定的，在靠近输入层的隐藏层中或会消失，或会爆炸。这种不稳定性是深度神经网络中基于梯度学习的根本问题。产生梯度不稳定的原因是反向传播算法。

    • 在反向传播过程中，我们通过链式法则来计算每个权重参数的梯度，这个梯度是损失函数相对于该权重参数的偏导数

      • 复合函数求导（链式法则）

        df(g(x))dx=df(g(x))dg(x).dg(x)dx\frac{df(g(x))}{dx} = \frac{df(g(x))}{dg(x)} . \frac{dg(x)}{dx}

      • 根据链式法则，假设有三层网络，对于第一层的某个权重参数 w1w_1，其梯度 ∂L∂w1\frac{\partial L}{\partial w_1} 可以表示为

      ∂L∂w1=∂L∂a2.∂a2∂z2.∂z2∂w1\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial a_2} . \frac{\partial a_2}{\partial z_2} . \frac{\partial z_2}{\partial w_1}

      • 其中，L 是损失函数，a2a_2 是第二层的激活输出，z2z_2 是第二层的加权输入。该链式法则会一直应用到网络的最后一层。如果网络足够深，这个乘积会变得更加复杂，涉及到更多的梯度相乘

      • 问题在于，如果乘法链中的任何一个梯度的值小于 1（例如 sigmoid 或者 tanh 函数），那么在多层网络中，这些梯度相乘的结果会随着层数的增加而急剧减小，导致梯度消失。而任何一个梯度的值大于 1，那么随着层数的增加，这些梯度相乘的结果会急剧增加，导致梯度爆炸

    • 所以，梯度的不稳定性主要是因为在反向传播过程中，浅层的梯度由深层的梯度的乘积决定导致的。这种不稳定性导致了梯度在网络中的传播过程中可能会变得非常小或非常大，从而使得网络的训练变得困难

  • 如何应对梯度的不稳定

    • 对于梯度消失

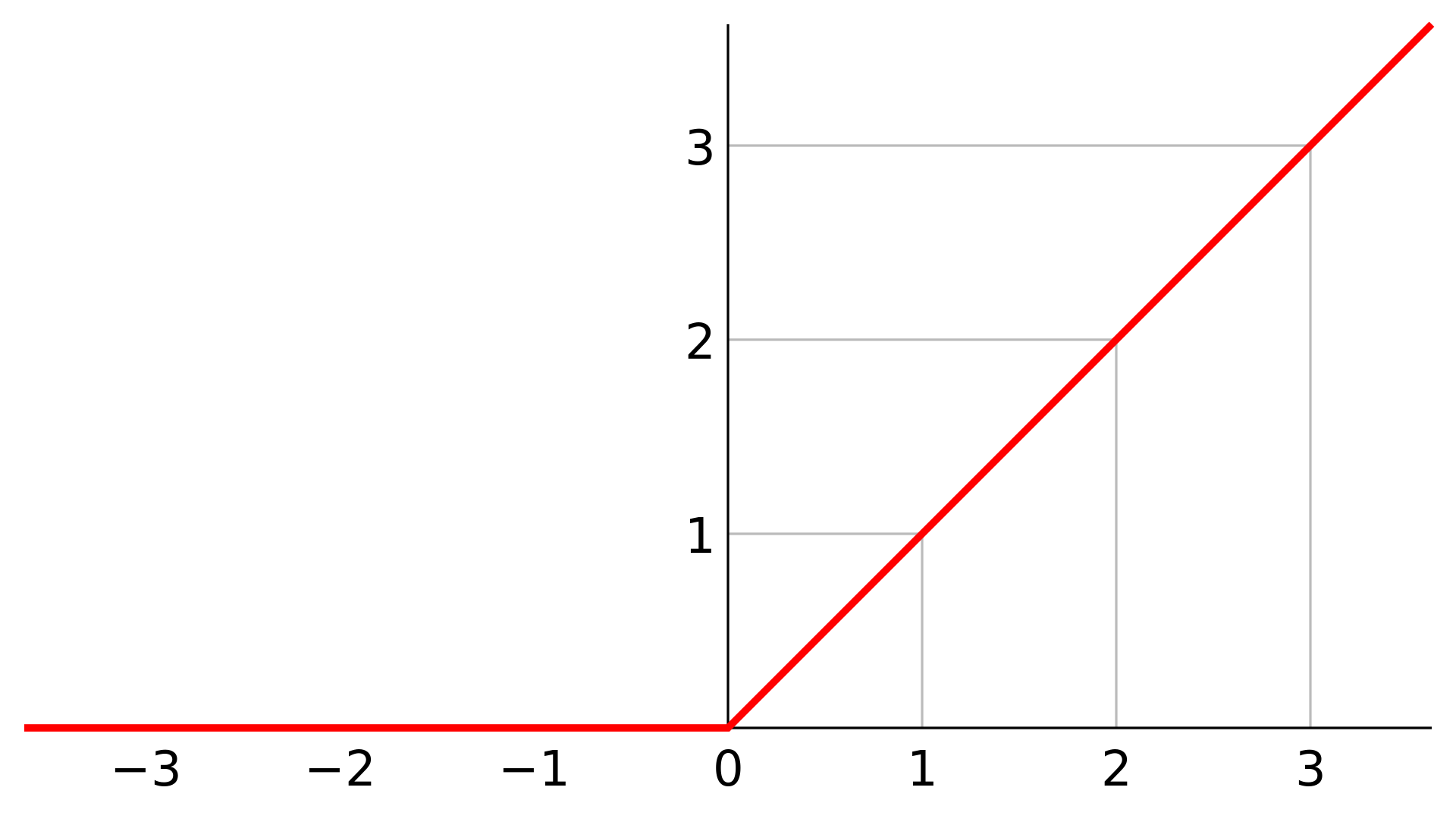
      1. 使用 ReLU 及其变种

        ReLU 在正区间的导数为常数，这有助于缓解梯度消失的问题

        alt text

      2. 权重初始化

        使用恰当的方法初始化网络权重，如 He 初始化或 Xavier 初始化，这些方法考虑了输入和输出的尺寸，以确保在训练初期激活值和梯度保持在恰当的范围

        • Xavier 初始化（Glorot 初始化）

          • Xavier 初始化是由

            Xavier Glorot 和 Yoshua Bengio 在2010年提出的。它适用于 sigmoid 和 tanh 激活函数。Xavier 初始化通过设置权重的初始值来保持输入和输出的方差一致，从而避免在多层网络中出现梯度消失或爆炸

          • 原理

            Xavier 初始化基于一个简单的观察：在多层感知机中，如果每一层的输入和输出的方差在传播过程中保持不变，那么网络的训练将更加稳定。这是因为梯度的方差在每一层之间应该是一致的，以确保梯度下降算法能够有效地更新权重

          • 算法

            对于一个权重矩阵 WW，其元素 ww 的初始值是从标准差为 ρ=2ninput+noutput{\rho} = {\sqrt{\frac {2} {n_{input} + n_{output}}}} 的正态分布中抽取的，其中 ninputn_{input} 是输入单元的数量，noutputn_{output} 是输出单元的数量。如果是均匀分布，则是 U(−6ninput+noutput,6ninput+noutput)U (- \sqrt {\frac {6} {n_{input} + n_{output}}}, \sqrt {\frac {6} {n_{input} + n_{output}}})

        • He 初始化（Kaiming 初始化）

          • He 初始化是由何恺明（Kaiming He）等人在2015年提出的，特别适用于 ReLU 激活函数。由于 ReLU 在正区间内梯度恒定，He 初始化考虑了这一点，并为权重设置了不同的初始值。其核心思想是保证在网络的前向传播和反向传播过程中，各层的输入信号方差大致相等，从而避免梯度消失或梯度爆炸问题，提高训练的稳定性和效率

          • 原理

            He 初始化方法的推导基于以下几个假设

            1. 权重独立同分布，且以 0 为中心对称分布

            2. 激活函数的线性区，对于 ReLU，其在正区间内的线性的，而负区间内是常数 0

            基于这些假设，He初始化方法推导出权重的方差应该与前一层和后一层的节点数有关。具体来说，对于一个全连接层，如果前一层有 nin_i 个节点，后一层有 ni+1n_{i+1} 个节点，那么权重的方差应该设置为 2ni\frac 2 {n_i}，这样做的目的是保证在前向传播和反向传播的过程中，各层的输入信号方差大致相等

          • 算法

            对于一个权重矩阵 WW，其元素 ww 的初始值是从标准差为 ρ=2ninput{\rho} = {\sqrt {\frac {2} {n_{input}}}} 的正太分布中抽取的，其中 ninputn_{input} 是输入单元的数量。如果是均匀分布则是 U(−6ninput,6ninput)U (- \sqrt {\frac{6} {n_{input}}}, \sqrt{\frac {6} {n_{input}}})

      3. 批量归一化

        批量归一化可以帮助归一化每层的输出，确保网络各层激活值分布一致，从而有助于梯度的稳定流动

      4. 使用残差连接

        使用残差网络（ResNet）结构，通过引入跳过连接（skip connections）允许梯度跨过某些隐藏层直接流动，这有效地避免了层级过多导致的梯度消失问题

      5. 贪心逐层无监督预训练（深度信念网络）（目前仅在 NLP 领域使用）

        • 论文链接

          https://proceedings.neurips.cc/paper_files/paper/2006/file/5da713a690c067105aeb2fae32403405-Paper.pdf

        • Hinton 为了解决梯度的问题，提出采取无监督逐层训练方法，其基本思想是把模型的每一层都视为受限玻尔兹曼机，每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程是逐层预训练

        • 在预训练完成后，再对整个网络进行“微调”（fine-tunning）。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优

        • 其中，受限玻尔兹曼机的训练采用的是对比散度算法（Contrastive Divergence），这种一种估计梯度的方法，用于最大化数据的对数似然值

    • 对于梯度爆炸

      1. 梯度裁剪

        通过设定一个阈值，将梯度的大小限制在这个阈值以内，这确保了在训练过程中梯度不会超过设定的最大值，从而避免了大幅更新权重

      2. 改变网络架构

        使用一些设计来防止梯度爆炸的网络结构，比如长短期记忆网络（LSTM）或门控循环单元（GRU），它们通过引入门控机制来控制信息的流动，可以有效缓解梯度爆炸问题

      3. 适当的权重初始化

        • 小随机值初始化

          权重可以从一个很小的随机分布中初始化，例如正态分布 N(0,ρ2)N(0, \rho^2) 或均匀分布 U(−ρ,ρ)U(-\rho, \rho)，其中 ρ\rho 是一个较小的标准差或范围，则有助于保持梯度的大小在可控范围内

        • Xavier 初始化 / He 初始化

          （见上文）

        • 正交初始化

          正交初始化通过确保初始化的权重向量之间是正交的（即它们的点积为零或接近零），来减少深度学习模型中梯度消失或梯度爆炸的风险；正交初始化的目的是在网络的初始阶段保持激活值和梯度的大小相对稳定，通过确保权重矩阵的列向量是正交的，可以减少不同权重更新之间的相互干扰，从而有助于梯度在网络中的传播

      4. 批量归一化

        批量归一化通过规范化中间层的激活也可以帮助控制梯度的规模，从而间接地减少梯度爆炸的风险

      5. 自适应学习率

        如Adam、Adagrad等算法，动态调整学习率以适应不同的梯度变化，这有助于控制梯度的大小并避免爆炸